Nuevamente 14 de marzo, el famoso día de π.

Éste es un humilde tributo a Arquímedes, por el tremendo esfuerzo que dedicó a calcular el valor de π - o al menos ponerlo en ciertos límites. En este artículo explico un poco su algoritmo, y luego lo pruebo en código.

Algoritmo de Arquímedes

Por esas casualidades de la vida (o no!), hace poco comencé a leer un libro sobre la historia del cálculo1 (por ahora viene bastante bien!) y me llamó la atención las anécdotas de las primeras aproximaciones de π. Especialmente la que hizo Arquímedes, famoso filósofo griego, porque fue el primero en hacerlo de una manera algorítimica.

Su método consistía en simplemente dibujar un polígono (hexágono) dentro de un círculo y calcular su perímetro. Ese valor debería aproximarse al de la circunferencia:

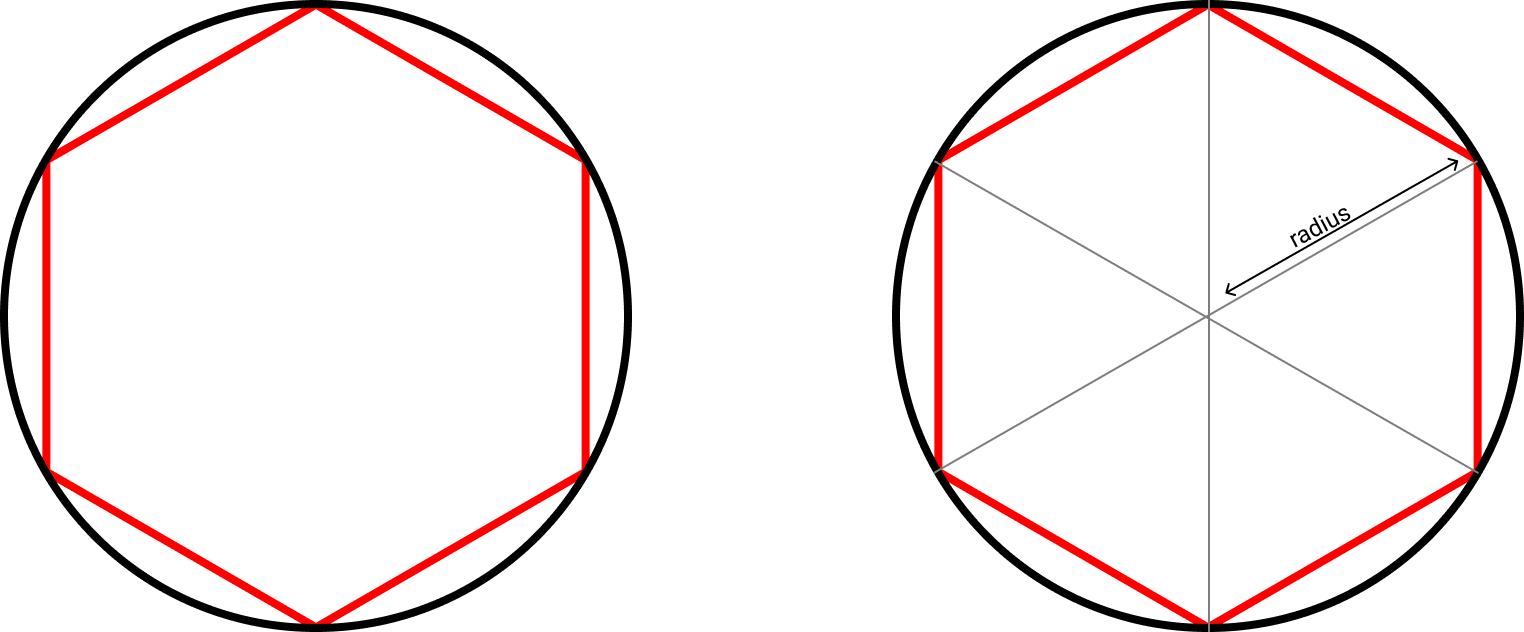
Un hexágono dentro de un círculo. Su perímetro es 6 veces el radio o 3 veces el diámetro.
Un hexágono dentro de un círculo. Su perímetro es 6 veces el radio o 3 veces el diámetro.

Usó un hexágono (en lugar otro polígono) por razones puramente prácticas. El hexágono se descompone en 6 triángulos equiláteros (los 3 lados iguales), y simplifica el cálculo. Es relativamente sencillo ver que si uno de los lados es radio, el perímetro del hexágono es 6 veces radio, o 3 veces diámetro. Como el hexágono está dentro del círculo, el cáculo resulta en número más chico que la circunferencia. Así, él supo que la proporción mágica entre el diámetro y la circunferencia (lo que llamamos π) no puede ser menor a 3. 3 es el límite inferior.

Siguiendo el mismo razonamiento, dibujando un hexágono que contenga el círculo (afuera, en lugar de adentro) se puede determinar el límite superior, un número que π no puede exceder.

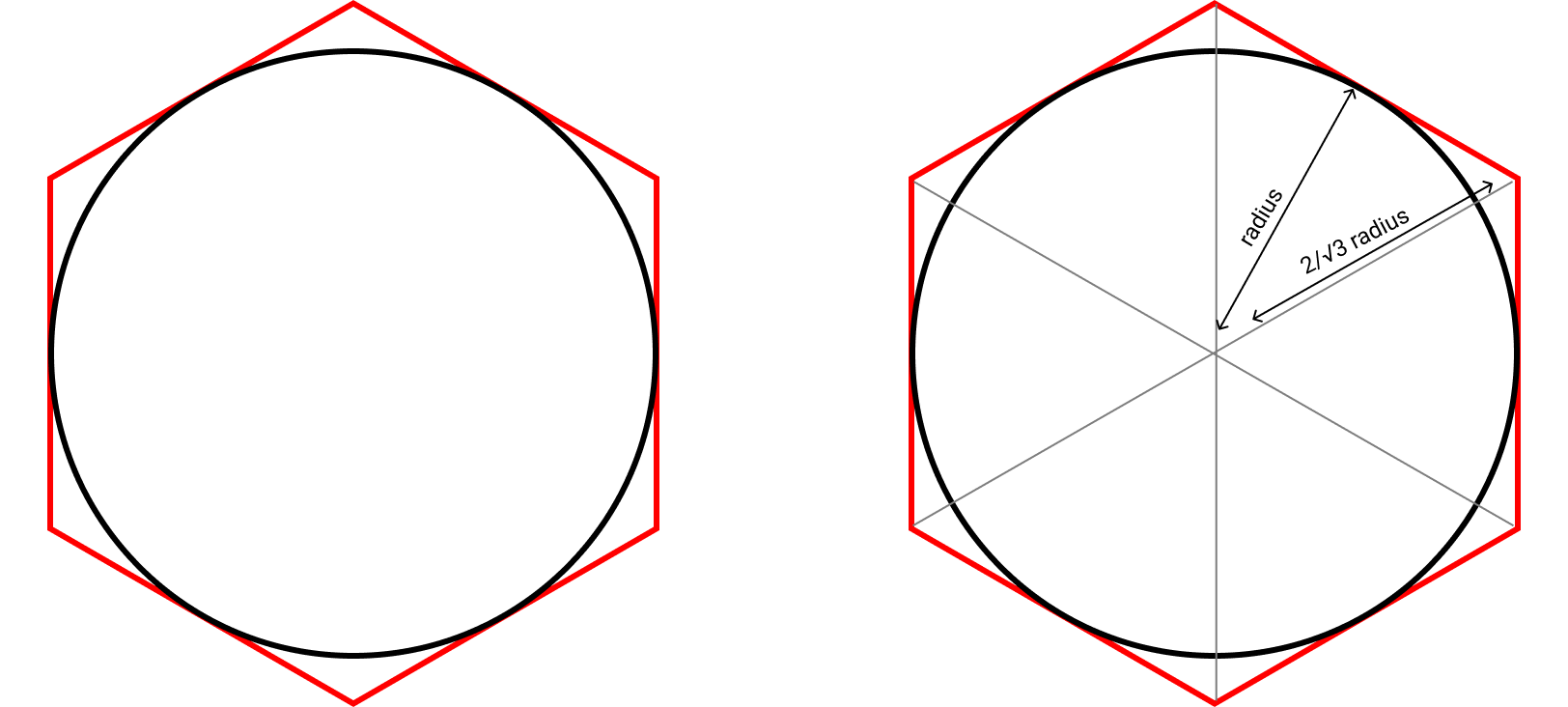
Un hexágono fuera de un círculo. Su perímetro es 12/√3 veces el radio, o 6/√3 veces el diámetro.
Un hexágono fuera de un círculo. Su perímetro es 12/√3 veces el radio, o 6/√3 veces el diámetro.

En éste caso el lado del triángulo es un poco mayor al radio. Pero usando el teorema de Pitágoras (ya conocido para ese entonces), calculó que que cada lado es 2/√3 veces el radio, y el perímetro por consiguiente es 6√3 veces el radio. En definitiva, el límite superior de π es 3.46410…

Hasta ahora, entonces, usando un hexágono obtuvo que: 3 < π < ~3.464. Bastante bien, eh.

Lo interesante es cómo siguió desde ahí (el algoritmo): continuó con la geometría pero subdividió cada triángulo en 2 (pasó de un hexágono a un dodecágono), arrimándolos hacia la circunferencia. Los dodecágonos (interno y externo) se verían así:

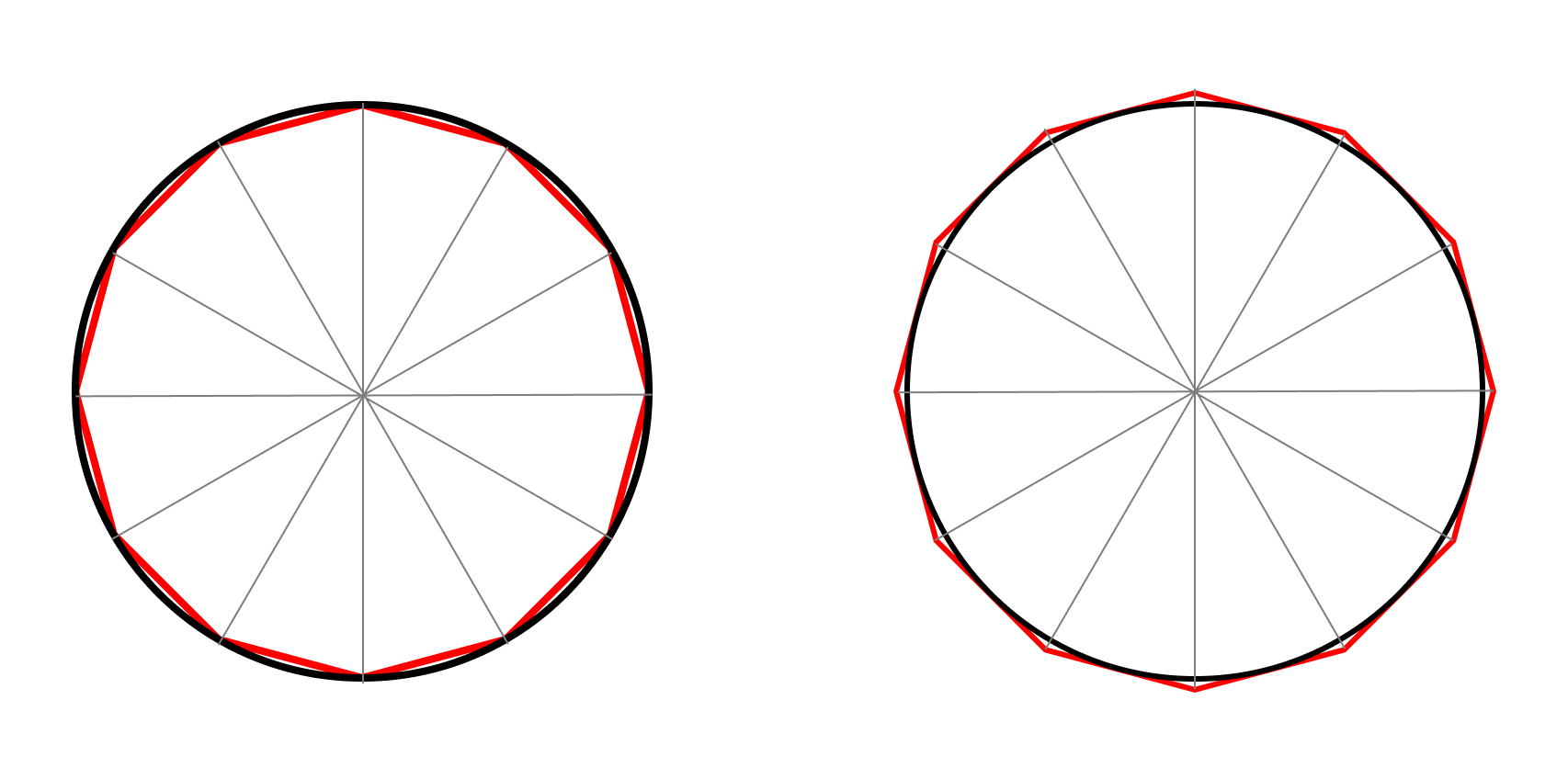
Un dodecágono (12-lados) adentro y otro afuera del círculo.
Un dodecágono (12-lados) adentro y otro afuera del círculo.

La leyes pitagóricas seguían aplicando, aunque las operaciones se ponían un poco más trabajosas (ángulos mas pequeños, raíces cuadradas… todo a mano!). Pero gracias a usar un polígono con más lados (12 en vez de 6), achicó el espacio entre el límites inferior y superior un poco más.

No se conformó con eso y tomó un paso más (polígono de 24 lados), y otro (48 lados), e incluso otro! Terminó trabajando con un polígonos de 96 lados! Un esfuerzo aritmético realmente heroico. Con éste 96-lados-polígono, pudo concluir que π se encuentra en algún lugar entre 3 + 10/71 y 3 + 10/70.

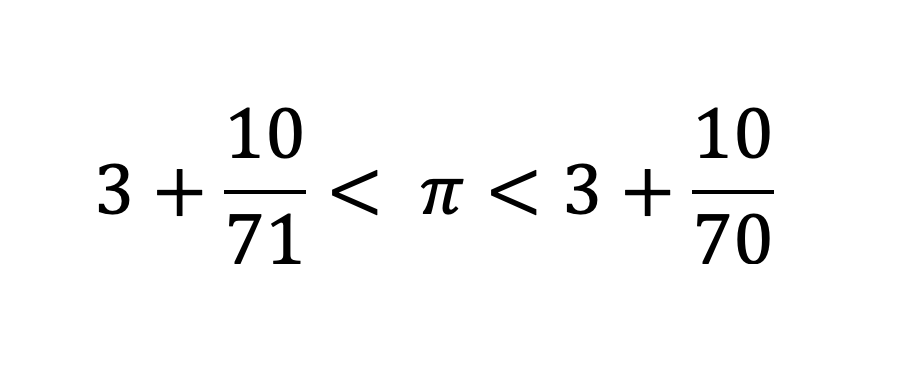
Límites de π obtenidos por Arquímedes usando un polígono de 96 lados.
Límites de π obtenidos por Arquímedes usando un polígono de 96 lados.

Fascinante.

(De hecho, ese límite superior (3+10/70) se puede escribir como 22/7, aproximación popular que se enseña hoy en día en las escuelas.)

En código

Creo que Arquímedes hubiese seguido subdividiendo los triángulos si el cálculo no fuese tan complejo. Seguramente intuía que incrementando los lados del polígino más y más, llegaría a un valor absoluto2 - o al menos la aproximación iba a mejorar3. Un trabajo durísimo para hacerlo a mano… pero hoy tenemos computadoras!

Me tomé la molestia de agarrar la pala y hacer un poco de geometría (?), para escribir el código. Claro, yo puedo utilizar las funciones seno y tangente - lujos que Arquímedes no tenía. Ahora puedo obtener aproximaciones de π tan precisas como quiera con sólo incrementar el número de lados del polígono.

Ésta es la geometría básica:

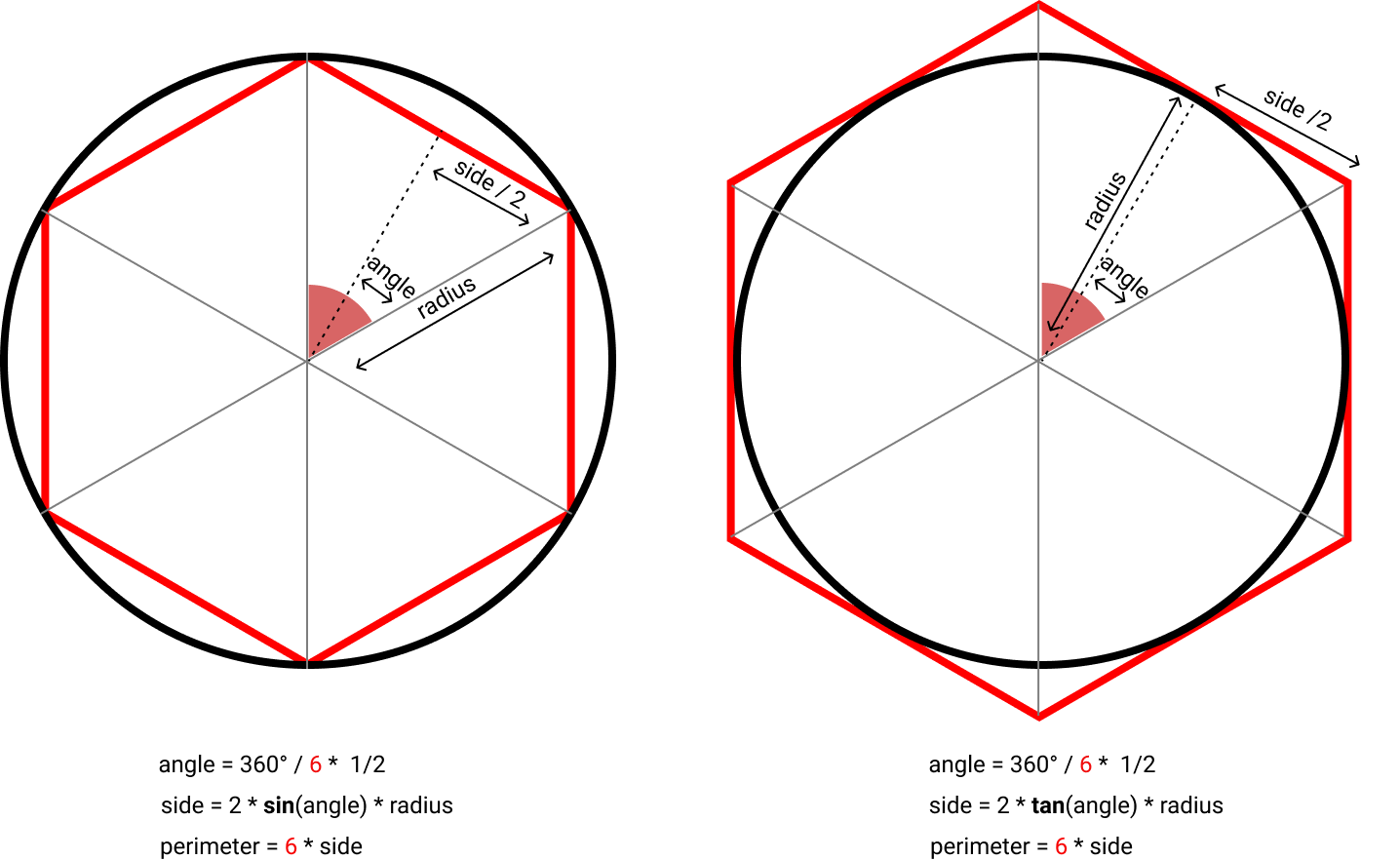
Geometry of the hexagon inside and the hexagon outside, expressed in terms of the number of sides (in red) and trigonometrical functions (sin and tan).
Geometry of the hexagon inside and the hexagon outside, expressed in terms of the number of sides (in red) and trigonometrical functions (sin and tan).

Éste es el código, que asume radio = 1 y aplica el algoritmo 10 veces:

from math import sin, tan, radians as r

def printPyBoundaries(n_gon: int) -> float :
	lower_bound = sin(r(360/(n_gon*2))) * n_gon
	upper_bound = tan(r(360/(n_gon*2))) * n_gon

	print('{}-gon = {} < π < {}'
			.format(n_gon, lower_bound, upper_bound))

n_sides = 6
for i in range(10):
	printPyBoundaries(n_sides)
	n_sides *= 2

Éste programa imprime lo siguiente:

6-gon = 2.9999999999999996 < π < 3.4641016151377535
12-gon = 3.105828541230249 < π < 3.2153903091734723
24-gon = 3.1326286132812378 < π < 3.1596599420975
48-gon = 3.1393502030468667 < π < 3.146086215131435
96-gon = 3.1410319508905093 < π < 3.142714599645368
192-gon = 3.1414524722854615 < π < 3.1418730499798233
384-gon = 3.1415576079118575 < π < 3.141662747056848
768-gon = 3.1415838921483177 < π < 3.141610176604689
1536-gon = 3.1415904632280496 < π < 3.1415970343215256
3072-gon = 3.1415921059992713 < π < 3.141593748771352

El significado de éstas líneas es el siguiente: con un polígono de 3072 lados, se puede conocer el valor de π con hasta 5 dígitos decimales de precisión: 3.14159.

Y eso es todo por hoy; felíz día de π!◆

  1. Infinite Powers. The Story of Calculus, The Language of the Universe. . Sorpresivamente entretenido! (link) ↩

  2. Los números irracionales no se consideraban “números” (mas bien “magnitudes”) y eran filosóficamente incómodos. ↩

  3. No existía el Cálculo en ese entonces (pasarían otros ~2000 años), pero su algoritmo contiene presagios: subdivide el problema en partes pequeñas (y todavía más pequeñas), las resuelve, y las integra nuevamente. ↩