Archimedes and π

Another March 14th - the famous π day!.

This is my humble Archimedes tribute, for his effort calculating π. In this post I explain his algorithm and translate it to code.

Archimedes Algorithm

By coincidence (or not), I started reading a book about the story of calculus¹ very recently (still enjoying it!). The stories of the first approximations of π quickly got my attention. Particularly the one from Archimedes, famous Greek philosopher, because he was the first person using an algorithmic method.

This method consisted in drawing an hexagon inside a circle, and calculate the perimeter of the hexagon… hoping this value approximates the circumference:

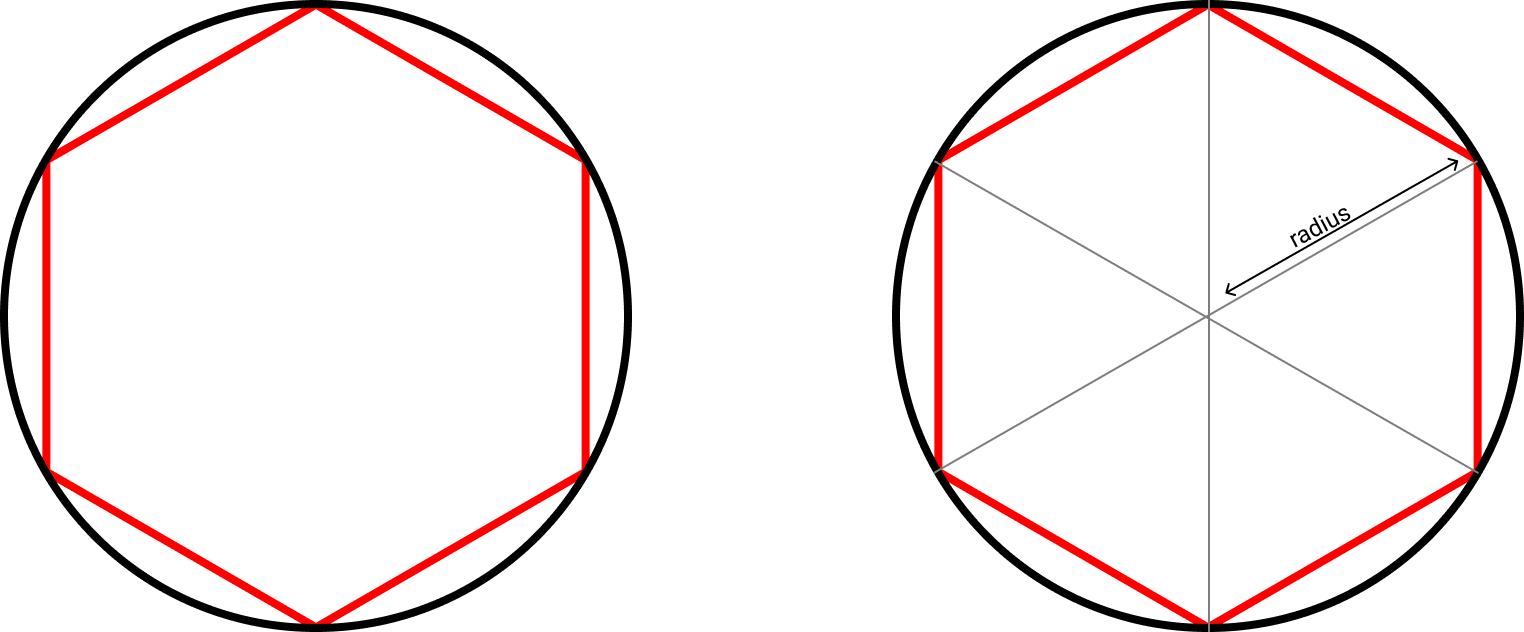
The reason for using hexagon and not other polygon was that an hexagon is made up of 6 equilateral triangles - all sides measure the same -, and that makes the math easy (the initial one at least). It’s relatively straight-forward to see that if one side is radius, the perimeter of the hexagon is 6 times radius, or 3 times diameter. Because the hexagon is inside the circle, the calculation surely falls short, but at least he knew that the magic proportion between diameter and circumference (what we call π) cannot be lower than 3; 3 becomes the lower bound.

With the same reasoning, drawing an hexagon just outside the same circle helped him to determine the upper bound, a value π can never exceed.

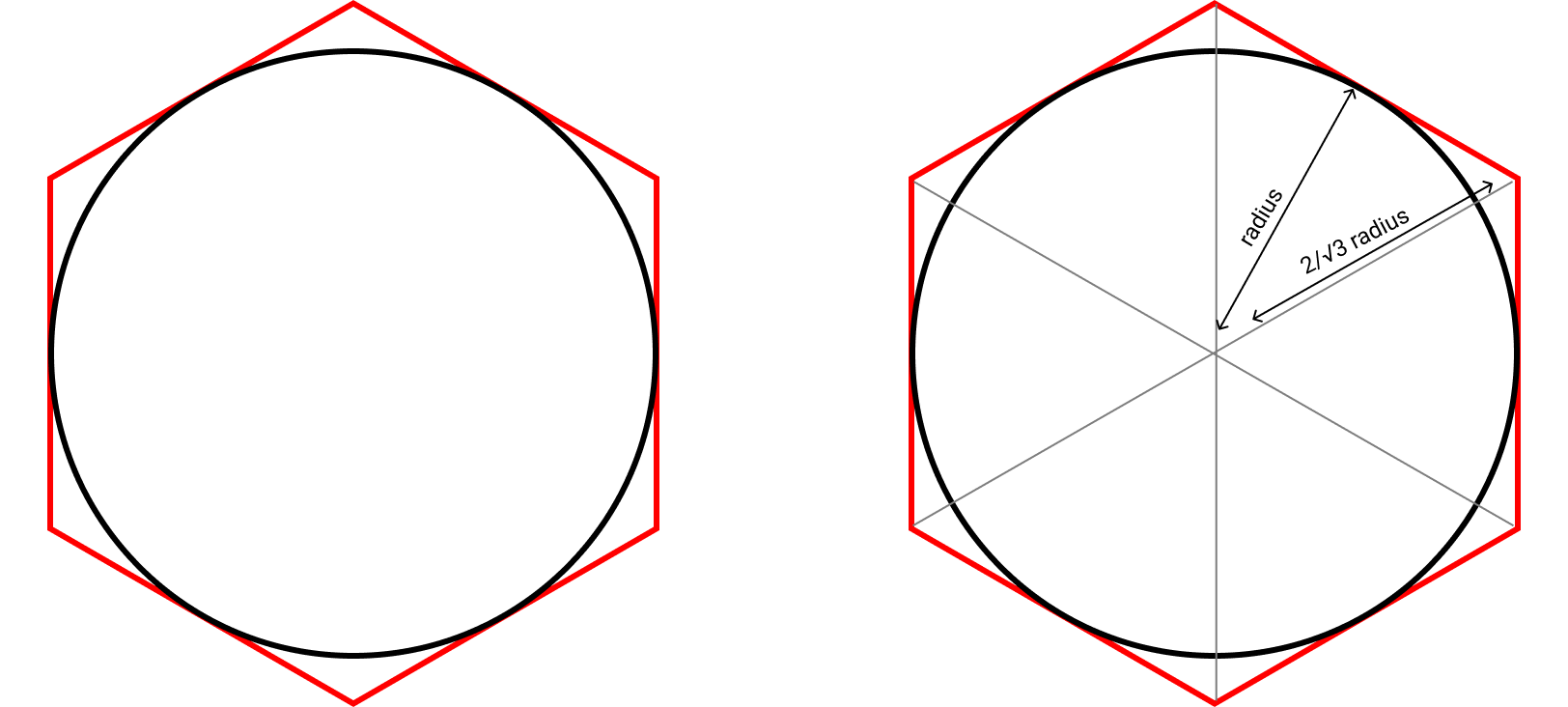
Here, the side is something slightly bigger than radius. Using Pythagoras theorem (well known by then), he determined that each side is 2/√3 times radius. The hexagon perimeter is then 6/√3 times diameter. In other words, the π upper value is 3.46410…

Until here: 3 < π < ~3.464. Good, huh.

For me, the interesting part is how he followed-up - the algorithm. He kept doing geometry but subdividing each triangle in 2 (from 6-gon to 12-gon) pulling the triangles closer to the circumference. The 12-gons would look like the following ones:

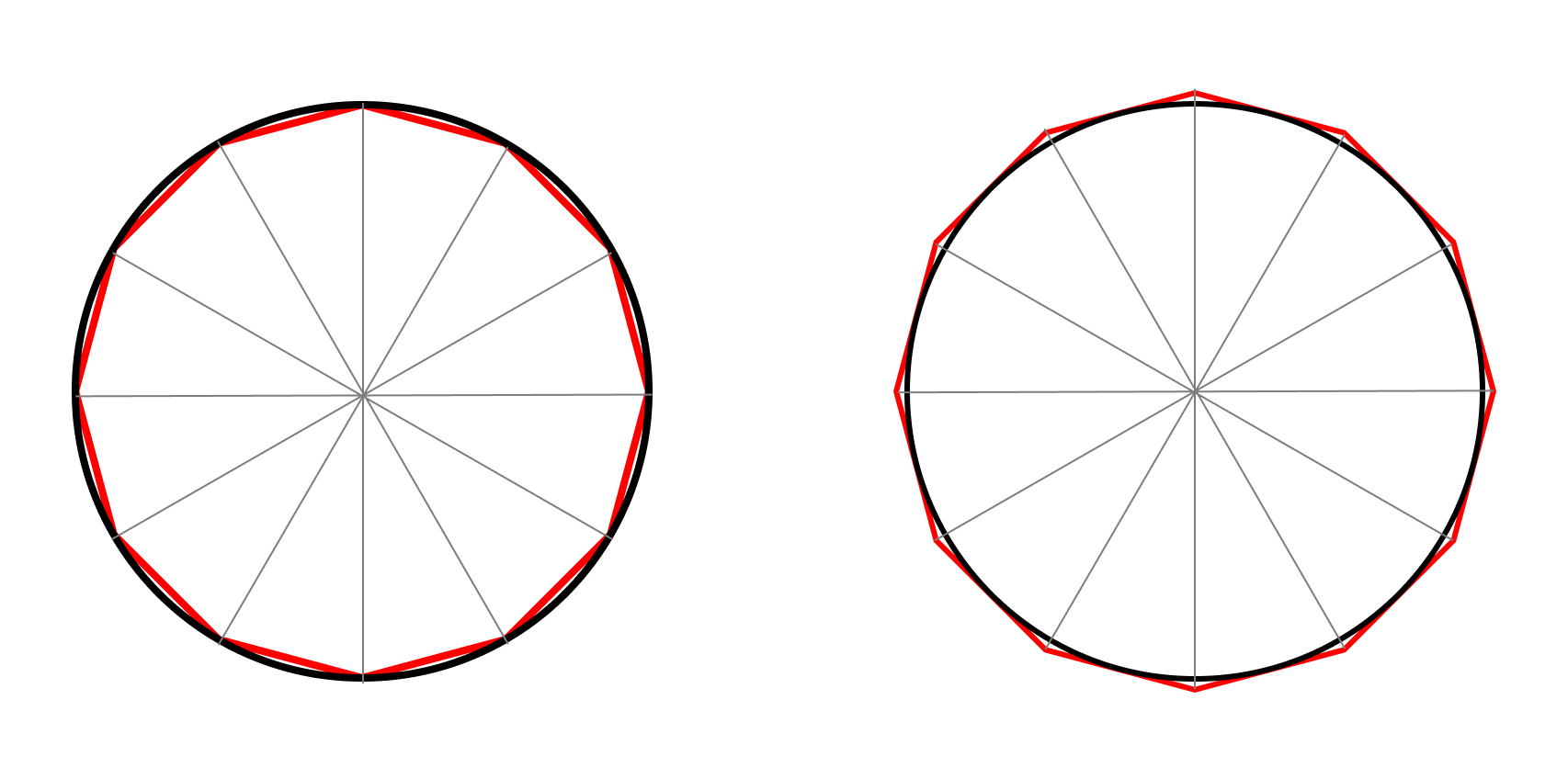
The pythagorean geometry was well known, but the operations became a bit more laborious (imagine all those smaller angles, square roots… all by hand!). But the reward was clear: he tightened the lower and upper bounds a bit more by using an 12-gon instead of an 6-gon.

He even went one step forward (24-gon), another (48-gon), and even another one! He worked with an 96-gon! His efforts were arithmetically heroic. By using a 96-gon inside and outside the circle, he got to the result that π is somewhere between 3 + 10/71 and 3 + 10/70.

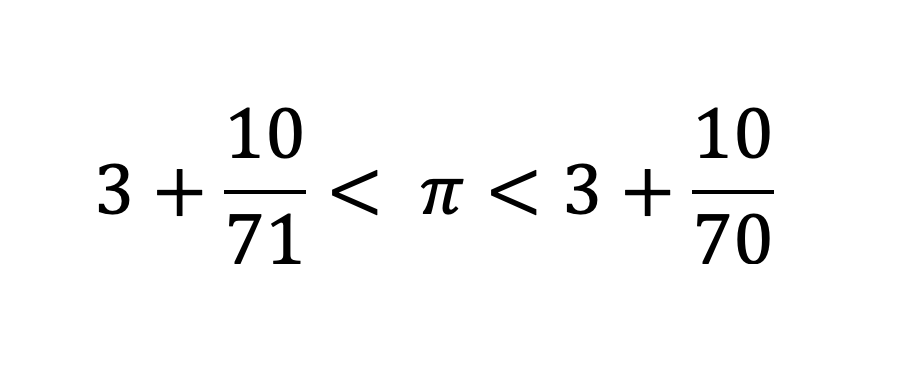
Truly fascinating.

(By the way, the upper bound (3+10/70) reduces to 22/7, a popular π approximation teached today at schools.)

Code the algorithm

I think Archimedes would have followed the process many more steps if that was easier to do. He probably thought one can keep breaking the polygon further until he gets to a final value ², or at least approximate π a bit more³. That’s a hard job to do by hand… but hey!, we have computers!

I’ve done some geometry and coded a short function in Python using sin and tan facilities - a luxury Archimedes didn’t have. I get “as good as desired” π approximations, by increasing the number of sides of the polygon.

Here’s the basic geometry:

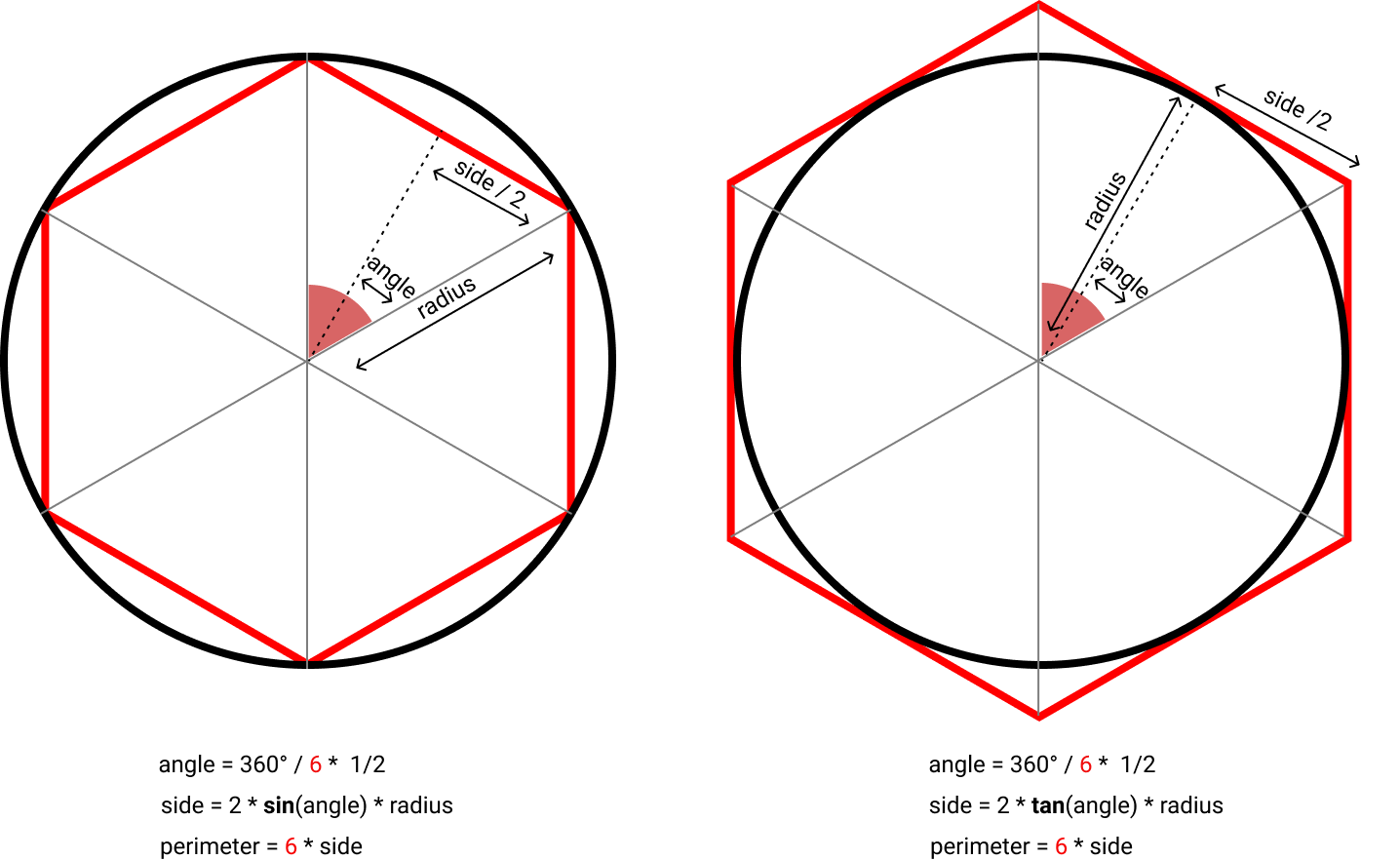
Here is the code. It assumes radius is 1, and applies the algorithm only 10 times:

from math import sin, tan, radians as r

def printPyBoundaries(n_gon: int) -> float :
	lower_bound = sin(r(360/(n_gon*2))) * n_gon
	upper_bound = tan(r(360/(n_gon*2))) * n_gon

	print('{}-gon = {} < π < {}'
			.format(n_gon, lower_bound, upper_bound))

n_sides = 6
for i in range(10):
	printPyBoundaries(n_sides)
	n_sides *= 2

The program above produces the following output:

6-gon = 2.9999999999999996 < π < 3.4641016151377535
12-gon = 3.105828541230249 < π < 3.2153903091734723
24-gon = 3.1326286132812378 < π < 3.1596599420975
48-gon = 3.1393502030468667 < π < 3.146086215131435
96-gon = 3.1410319508905093 < π < 3.142714599645368
192-gon = 3.1414524722854615 < π < 3.1418730499798233
384-gon = 3.1415576079118575 < π < 3.141662747056848
768-gon = 3.1415838921483177 < π < 3.141610176604689
1536-gon = 3.1415904632280496 < π < 3.1415970343215256
3072-gon = 3.1415921059992713 < π < 3.141593748771352

This means that, using an 3072-gon, one can get 5 decimal digits of precision of π: 3.14159.

Have a happy π day!◆