Happy π Day!

Como seguramete te enteraste por todos lados, hoy es el día del número π. La razón es simple: hoy es el 3/14. Claro, teniendo en cuenta que el mes está escrito antes que el día. O sea, para los EEUU y un par de islas del Pacífico (posta).

No importan esos detalles, es un día en dónde se “celebra” eso. Cómo? Ni idea. Pero no por eso hay que desmerecerlo.

El número PI tiene muchísimas implicaciones en el universo; las matemáticas hacen uso exhaustivo de él. Algunos también se van de mambo y le atribuyen “poderes” y cosas así. Pero quitémosle el misterio: π es la relación entre una circunferencia y su diámetro: cuántas veces se repite el diámetro en ella. También, π es un número irracional, lo que significa que tiene infinitos valores decimales. Dicho de otra manera: no se lo puede escribir completamente porque siempre hay más cifras que agregar después de la coma (hola doña rosa).

Lo curioso es que a lo largo de la historia, muchas personas se dedicaron a calcularlo, intentando llegar a una mayor precisión (más cifras decimales). Quizás para ver si se podía llegar a algún final.. o no, no lo sé. Pero sí sé que fué y será algo divertido (?) de hacer.

Cómo se hace para calcular π? Hay muchas maneras: métodos manuales, de cálculo, con fracciones, etc.

Pero hoy, señoras y señores, les traigo un método totalmente novedoso. Así es! N U E V O.

Bueno, no. En realidad, nos lo explicó un profesor hace varios años ya. Nunca lo implementé, pero todavía lo recuerdo… Será que π afecta la memoria positivamente? (?)

Este método se basa en la estadística, y lo podría realizar cualquier ser humano. Me corrijo: cualquier ser humano que sepa marcar el piso, arrojar algo, sumar y dividir :)

Requisitos:

• Escoger un palo. El largo del palo no importa.
• Marcar el suelo con líneas paralelas. La distancia entre ellas es el largo del palo.
• Tener un papel y lápiz para contar dos cosas: TIROS y CRUCES.

Con eso listo, repetir los siguientes pasos:

1. arrojar el palo aleatoriamente (que el lugar donde caiga y su orientación lo sean).
2. observar el palo en el suelo: está tocando el palo alguna de las líneas?
3. En el papel
   • +1 en el número TIROS
   • +1 en el número CRUCES, SOLO SI el palo toca/cruza alguna línea.

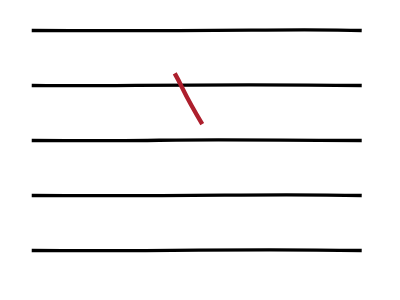
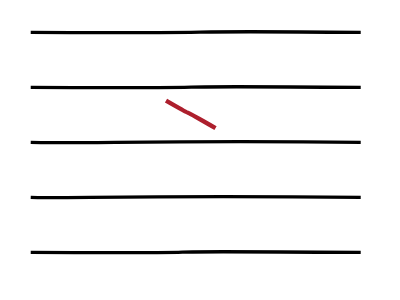
• Repetir los pasos 1, 2 y 3; repetir, repetir. Muchísimas veces. Cuantas más, mejor!

• Y finalmente: Hacer la división entre TIROS y CRUCES (veces tiradas sobre veces en que tocó una línea). Esa cuenta da como resultado… π/2! (1.57079632679..). Increíble, no?

La clave está en la aleatoriedad de las tiradas. Y porsupuesto, la precisión del número será mejor cuanto mayor sea el número de intentos.

Para comprobar lo que dije anteriormente, les dejo unas líneas de Python que intenta representar ¹ la misma idea.

import random
import math

# NOTES:
# * there are 5 lines marked in the floor
# * the random position is only relevant in one axis
# * the lenght of the stick is one; so the lines are marked 
# with floor() function

ATTEMPTS = 1000000

throws  = 0
touched = 0

while throws < ATTEMPTS:
    throws += 1

    angle = random.random() * math.pi
    tipL  = random.random() * 5
    tipR  = tipL + 1 * math.sin(angle)

    if int(math.floor(tipL)) != int(math.floor(tipR)):
        touched += 1

print("ATTEMPTS:   %d" % ATTEMPTS )
print("real:       %.8f" %  1.57079632679)
print("calculated: %.8f" %  ( float(throws) / touched ))

Como pueden ver, al final del ciclo imprimo el valor calculado junto al “real” (algunas cifras) para que se vea cuánto se aproxima.

La precisión varía cambiando el valor de ATTEMPTS. Salud!.-